Mountain Car Continuous
A DDPG-based RL method.
This project was completed by myself.
Abstract
This model is based on DDPG Reinformcement Learning Algorithm. Our goal is let the car go upon the hill to reach the flag. However, the momentum of the car cannot support the car to go directly to the top at a time. Thus, the car need to use the hill on the left to accelerate itself to rush upon the right hill to reach the flag.
The main problem is that the penalty of movement may cause the car to stay still and not taking any action. This is because the positive reward is too difficult to reach and the penalty of exploring is too high. Generally, if the car never reaches the flag, it will eventually choose to stay still.
My solution to solve this problem is adding a descending random propelling (which is considered as noise) to the action that the neural network is generating. By doing this, we can literally “propel” the car to go, so that it cannot stay still.
Mountain Car MDP
The Mountain Car MDP is a deterministic MDP that consists of a car placed stochastically at the bottom of a sinusoidal valley, with the only possible actions being the accelerations that can be applied to the car in either direction. The goal of the MDP is to strategically accelerate the car to reach the goal state on top of the right hill. There are two versions of the mountain car domain in gymnasium: one with discrete actions and one with continuous. We will experiment with the continouse version in this one.
The observation is a ndarray with shape (2,) where the elements correspond to the position of the car along the x-axis and the velocity of the car.
The action is a ndarray with shape (1,), representing the directional force applied on the car. The action is clipped in the range [-1,1] and multiplied by a power of 0.0015.
A negative reward of $-0.1 * action^2$ is received at each timestep to penalise for taking actions of large magnitude. If the mountain car reaches the goal then a positive reward of +100 is added to the negative reward for that timestep.
You can read more the MountainCar Continous environment here
Continuous Action Spaces
It’s conceptually the same as for discrete action spaces. In discrete action spaces you have a discrete distribution like the categorical distribution and you calculate the log pi probabilities using its mass function. In continuous action spaces you use a continuous distribution like the Gaussian distribution and calculate the log pi “probabilities” using its density function. Everything else is the same.
So instead of having network that outputs the parameters for a categorical distribution, you have a network that outputs parameters for (usually) a Gaussian distribution (i.e. the mean and standard deviation)
But, usually we just output the mean using a neural network, and have a separate set of learnable parameters for std (in log space) for each action. For example, if we 3 continous actions then we will have a neural network which will output the means for these actions and then separate 3 parameters which will represent the log std of these actions. We still learn these log std but they are not dependent on state. We just have a log std for each action.
Other approaches for std include:
- Having a std as output of neural network just as the mean.
- Initializing some std for all actions at start and then steadily decrease if using a std_decay hyperparameter as the training progresses.
Deep Deterministic Policy Gradient (DDPG) Algorithm
The stochastic policy gradient calculating formula based on Q value is: \(\nabla_\theta J(\pi_\theta) = E_{s\sim\rho ^ \pi,a\sim \pi_\theta}[\nabla_\theta \log \pi_\theta (s,a)Q_\pi(s,a)]\)
The deterministic policy gradient calculating formula based on Q value is: \(\nabla_\theta J(\pi_\theta) = E_{s\sim\rho ^ \pi}[\nabla_\theta \pi_\theta (s) \nabla_a Q_\pi(s,a)|_{a=\pi_\theta (s)}]\)
DDPG Brief Principle
Very generally speaking, DDPG Algorithm is a combination of DQN Algorithm and Actor-and-Critic Algorithm. Where both actor network and critic network are separated into policy network and target network. So, there will be 4 neural network in total.
More Specifically…
DDPG has 4 networks: Actor Current network, Actor target network, Critic Current network, Critic target network. The structure of the two Actor networks is the same, and the structure of the two Critic networks is the same.
The current Q network of DQN is responsible for using ϵ− greedy method to select the action \(A\) for the current state \(S\), perform the action \(A\), obtain the new state \(S'\) and reward \(R\), put the sample into the experience replay pool, and use greedy method to select the action \(A\) for the next state \(S'\) sampled in the experience replay pool, so that the target Q network can calculate the target Q value. After the target Q network has calculated the target Q value, The current Q network updates network parameters and periodically copies the latest network parameters to the target Q network.
By analogy with DQN, the current network of Critic in DDPG, the target network of Critic and the current Q network of DQN, the functional positioning of the target Q network is basically similar. However, there is no need to be greedy when selecting an action, and it is done with the Actor current network. The greedy method is used to select the action \(A\) for the next state \(S'\) sampled in the experience replay pool. This part of the work is used to estimate the target Q value, so it can be completed in the Actor target network.
-
Actor Current network: Responsible for the iterative update of policy network parameters \(\theta\), responsible for selecting the current action \(A\) according to the current state \(S\), for interacting with the environment to generate \(S'\) and \(R\).
-
Actor Target Network: Responsible for selecting the optimal next action \(A\) based on the next state \(S'\) sampled in the experiential replay pool. Network parameters are periodically replicated.
-
Critic Current network: Responsible for the iterative update of the value network parameter \(w\), responsible for calculating the current Q value \(Q(S,A,w)\).
-
Critic Target network: Responsible for calculating the target Q value. Where \(Q' = R + \gamma Q'(S', A', w')\)
Additionally, the way DDPG copies the current network parameters to the target network has changed.
In DQN, we copy the parameters of the current Q network directly to the target Q network. (A hard copy)
But now we need a soft copy to update the parameters.: \(w' \leftarrow \tau w + (1-\tau)w'\)
\[\theta' \leftarrow \tau \theta + (1-\tau)\theta'\]At the same time, in order to add some randomness to the learning process and increase the coverage of learning, DDPG will add some noise \(N\) to the selected actions, that is, the expression of the final action \(A\) interacting with the environment is:
\[A = \pi_\theta(s) + N\]And this is considered to be the propelling.
For the Critic Current network, the loss function is basically the MSE loss.
For the Actor Current network, the loss gradient is: \(\nabla_J (\theta) = \frac{1}{m}\sum_{j=1} ^ m [\nabla_a Q(s_i,a_i,w)|_{s=s_i,a=\pi_\theta(s)}\nabla_\theta \pi_\theta (s)|_{s=s_i}]\)
Actor Neural Network
class Actor(nn.Module):
def __init__(self, state_size, action_size):
super(Actor, self).__init__()
self.linear1 = nn.Linear(state_size, 32)
self.linear2 = nn.Linear(32, 32)
self.linear3 = nn.Linear(32, action_size)
self.reset_parameters()
def reset_parameters(self):
self.linear1.weight.data.normal_(0, 1e-1)
self.linear2.weight.data.normal_(0, 1e-1)
self.linear3.weight.data.normal_(0, 1e-2)
def forward(self, state):
x = state
x = self.linear1(x)
x = F.relu(x)
x = self.linear2(x)
x = F.relu(x)
x = self.linear3(x)
return torch.tanh(x)
Critic Neural Network
class Critic(nn.Module):
def __init__(self, state_size, action_size):
super(Critic, self).__init__()
self.linear1 = nn.Linear(state_size + action_size, 64)
self.linear2 = nn.Linear(64, 64)
self.linear3 = nn.Linear(64, 1)
self.reset_parameters()
def reset_parameters(self):
self.linear1.weight.data.normal_(0, 1e-1)
self.linear2.weight.data.normal_(0, 1e-1)
self.linear3.weight.data.normal_(0, 1e-2)
def forward(self, state, action):
x = torch.cat((state, action), dim=1)
x = self.linear1(x)
x = F.relu(x)
x = self.linear2(x)
x = self.linear3(x)
return x
DDPG Agent
class Agent:
def __init__(self, state_size, action_size, buffer_size, batch_size, gamma, tau):
# Actor Network and Target Network
self.actor = Actor(state_size, action_size).to(device)
self.actor_target = Actor(state_size, action_size).to(device)
self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=1e-3)
# Critic Network and Target Network
self.critic = Critic(state_size, action_size).to(device)
self.critic_target = Critic(state_size, action_size).to(device)
self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=1e-3)
# copy weights
self.hard_update(self.actor_target, self.actor)
self.hard_update(self.critic_target, self.critic)
self.memory = Memory(buffer_size, batch_size)
self.gamma = gamma
self.tau = tau
self.std = 1 # A parameter that will descend to calculate the noise
def hard_update(self, target, network):
for target_param, param in zip(target.parameters(), network.parameters()):
target_param.data.copy_(param.data)
def soft_update(self, target, network):
for target_param, param in zip(target.parameters(), network.parameters()):
target_param.data.copy_(self.tau*param.data + (1-self.tau)*target_param.data)
def learn(self, batch):
state, action, reward, next_state, done = batch
state = torch.tensor(state).to(device).float()
next_state = torch.tensor(next_state).to(device).float()
reward = torch.tensor(reward).to(device).float()
action = torch.tensor(action).to(device)
done = torch.tensor(done).to(device).int()
# update critic
next_action = self.actor_target(next_state)
Q_target = self.critic_target(next_state, next_action).detach()
Q_target = reward.unsqueeze(1) + (self.gamma*Q_target*((1-done).unsqueeze(1)))
critic_loss = F.mse_loss(self.critic(state, action), Q_target)
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# update actor
action_prediction = self.actor(state)
actor_loss = -self.critic(state, action_prediction).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# update actor_target and critic_target
self.soft_update(self.critic_target, self.critic)
self.soft_update(self.actor_target, self.actor)
def act(self, state, noise = True):
state = torch.tensor(state).to(device).float()
action = self.actor(state).cpu().data.numpy()
if noise:
noise = np.random.normal(0, self.std)
action = action + noise
if action[0] > 1:
action[0] = 1
if action[0] < -1:
action[0] = -1
return action
def step(self, state, action, reward, next_state, done):
self.memory.push((state, action, reward, next_state, done))
if len(self.memory) >= self.memory.batch_size:
self.learn(self.memory.sample())
def save(self):
torch.save(self.actor, "actor.pkl")
torch.save(self.critic, "critic.pkl")
def test(self):
new_env = make("MountainCarContinuous-v0")
new_env.seed(9)
reward = []
for i in range(50):
state = new_env.reset()
local_reward = 0
done = False
while not done:
action = self.act(state, noise = False)
state, r, done, _ = new_env.step(action)
local_reward += r
reward.append(local_reward)
return reward
Training Process
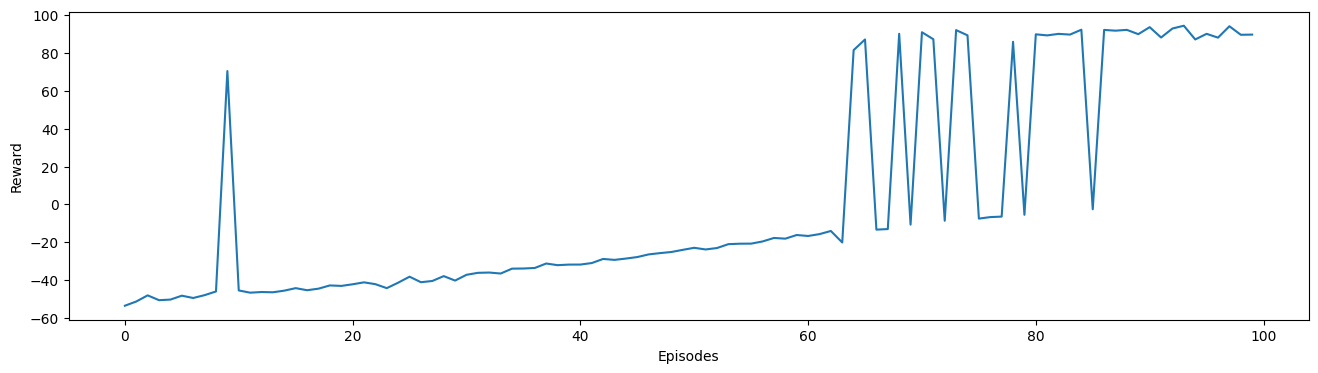
Result
The final effect of DDPG is shown as below:
For more information, see the work in my github repository!