Handwriting Formula Recognition

An image-to-latex inspired framework, transforming handwriting formula images into LaTeX-based context.

This project was cooperated with Y.L. Li, S. Yang, Z.Y. Tan and W. Liu.

Introduction

This project aims to solve the problems of recognizing pure LaTeX formulas as well as text-mixed formulas. During the project, we applied ResNet+Transformers framework. Additionally, we tried to optimize the hyperparameters and researched on the behavior changes according to these hyperparameters.

Data Preprocessing & Data Loading

Firstly, we tried custom datasets that were consisted of txt files and lst files. However, such method caused a highly redundant step which is reading txt files into the cache memory. For each single data, a file-reading operation was needed.

Thus, we changed the datasets’ hierarchy, following the format of image-to-latex framework. The whole datasets were divided into an original dataset (only includes images), a simple lst file that contains all labels and 3 filters, which were formatted as lst files. During the train process, the label file is read into the cache, then the filters will map all the images to its corresponding labels.

Model

We deployed ResNet+Transformers framework with the structure shown as below:

Figure 1&2. The framework of model.

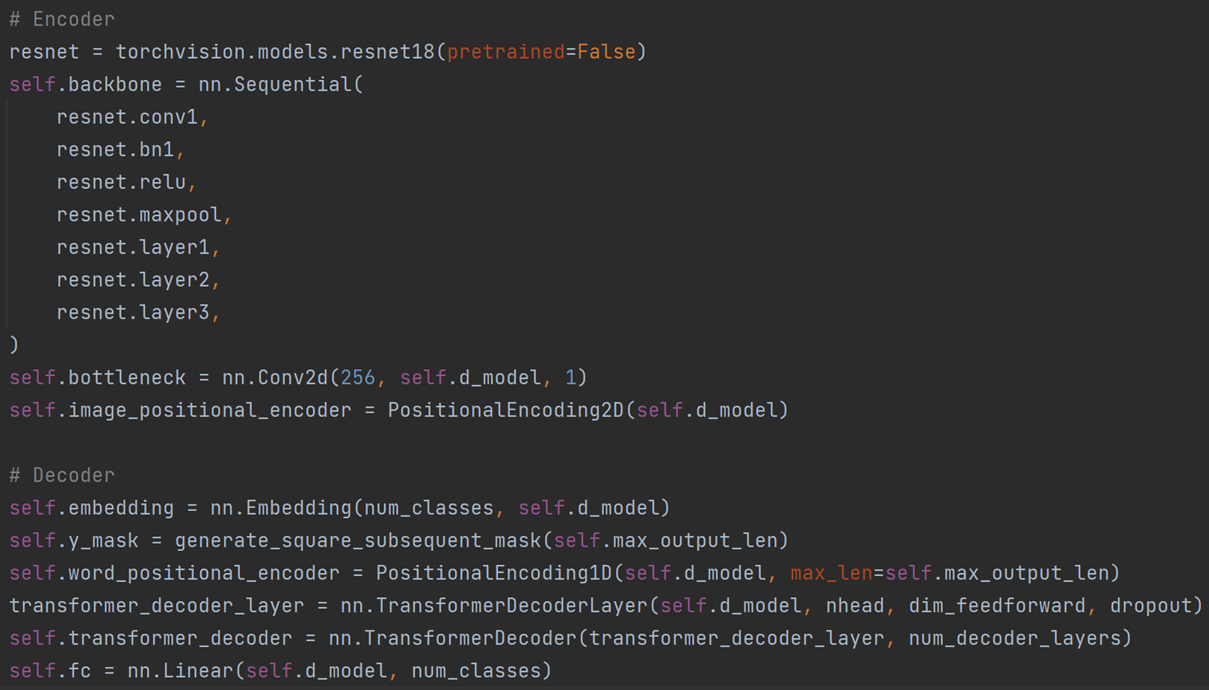
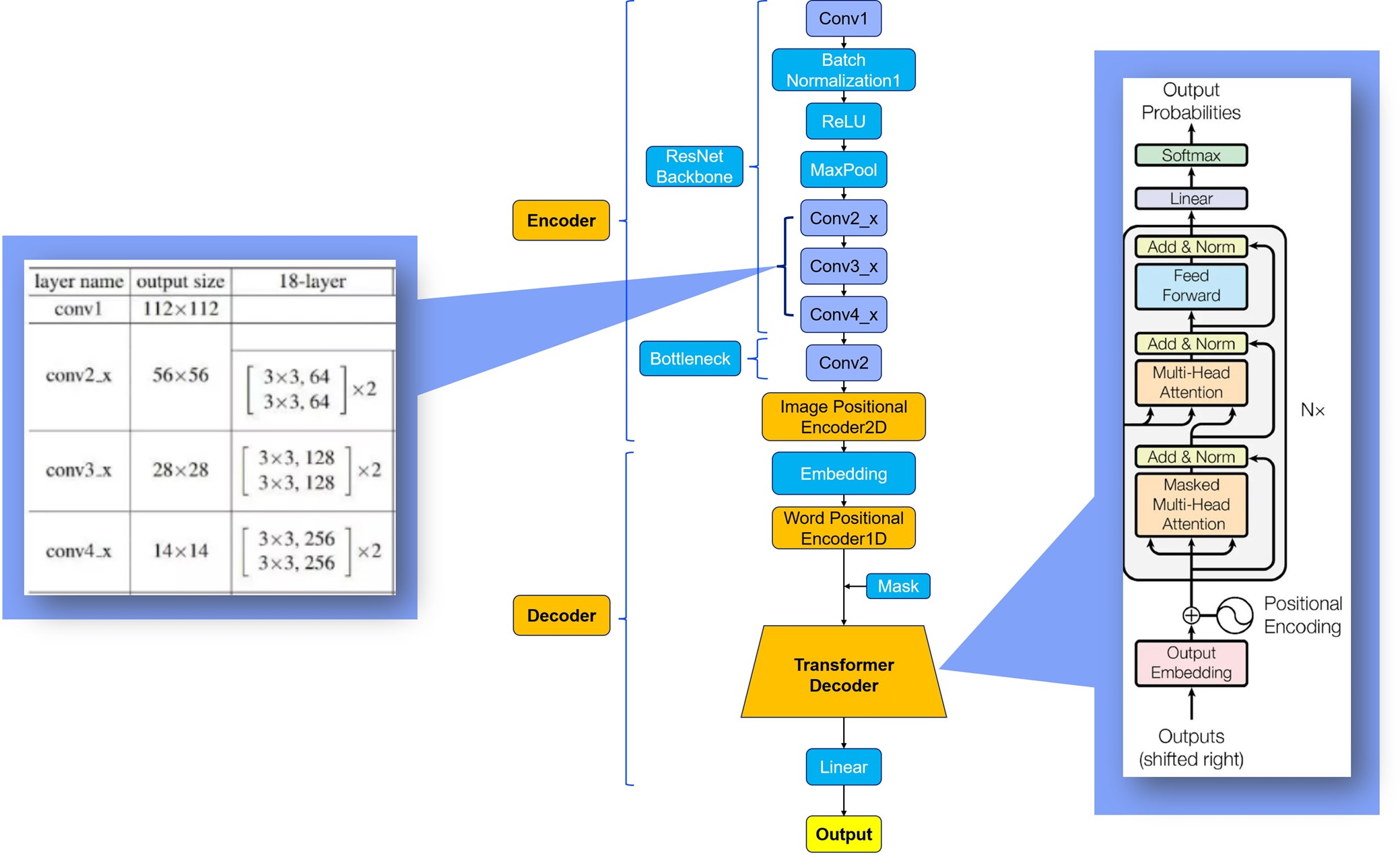
At first, we used the original model structure of the image-to-latex project for training. However, because this project is a mixed recognition of text formulas, the size of the new vocabulary was 4 times that of the original vocabulary after generating the vocabulary, and because the training results were not very satisfactory, there were often redundant output in the prediction results. Based on the experience during training, we speculate that this is also the manifestation of underfitting of the model. However, as the amount of training continued to increase, the performance of the model on the test set decreased, showing signs of fitting. We believe that this is because the neural network determines that the category of words to be output has increased too much, and the learning ability of the original model is insufficient.

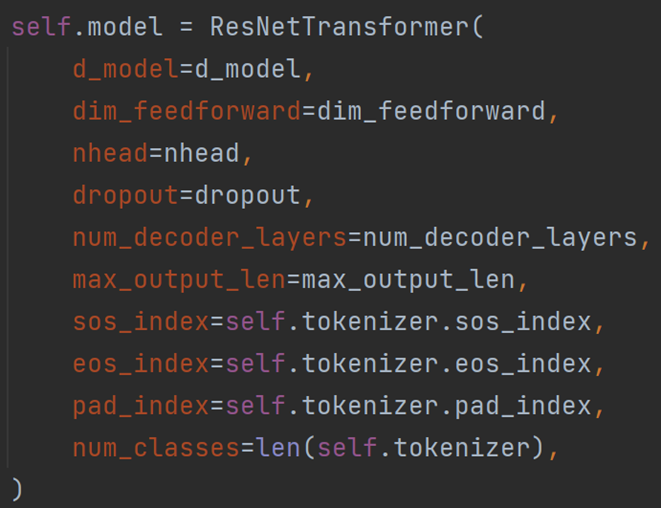
Therefore, we adjusted the parameters of the model in the configuration file, increasing the number of Decoder sub-layers in Transformers Decoder from 3 to 5, and re-trained the modified model. The final performance of the predicted result of the model has been improved, which may be further improved.

Figure 3&4. The parameter configuration of our framework.

Training & Fine-tuning

New Vocabulory

In the initial training of the pure mathematical expression recognition model, we used the original vocabulary of the image-to-latex model for training, but the training results were not satisfactory. The model would output unknown characters or blank characters for the input data, and it was usually unable to learn completely for a long input.

In addition to the lack of training of the model due to the insufficient number of epochs at the early stage of training, by re-observing the vocabulary and data set, we found that there are two problems: the original vocabulary of the image-to-latex model is incomplete, and the model cannot accurately learn symbols that do not appear in the vocabulary; And there are still a few Chinese characters in the data set of pure mathematical expressions. So we regenerated a complete vocabulary of numbers, English letters, mathematical symbols, and the Chinese characters that appeared in the dataset. For a dataset of mixed recognition of literal and mathematical expressions, we also regenerate a complete vocabulary.

Figure 5. Generating new vocabulory for our tasks.

Parameter adjustment

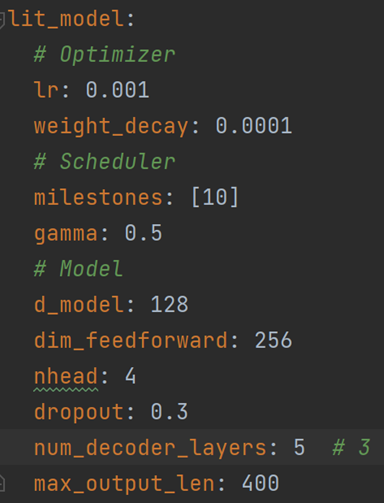
Due to the lack of hardware conditions, mainly due to the limitation of GPU memory size, the GPU cannot load a large batch. Therefore, for the pure mathematical expression recognition model, the batch size is adjusted to 16, and the remaining parameters are trained according to the default parameters of the image-to-latex model. Although the simple reduction of batch size solves the problem of insufficient GPU memory, it also creates new problems:

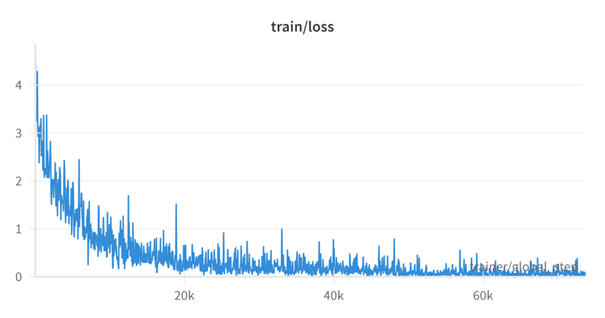
(1) The gradient oscillation is severe, the model converges slowly, and the epoch cannot be fully trained after more times.

Figure 6. Train loss on pure LaTeX formula recognition model, Learning rate=0.001.

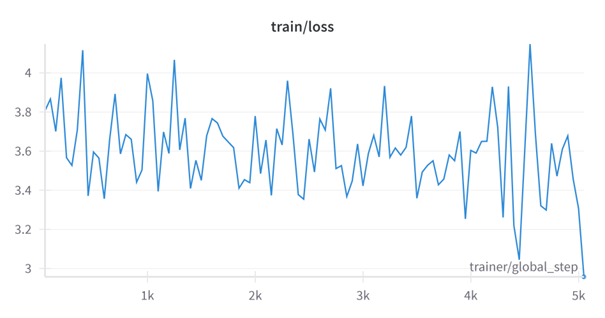
As shown in the figure above, the loss value of the model fluctuates severely, and the loss value of the training set still shows no obvious sign of decreasing after training with two epochs.

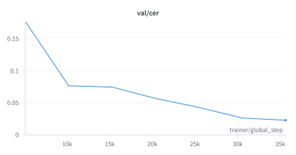
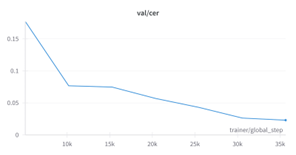
In this respect, we scaled the learning rate and the batch size in the same proportion according to the linear scaling principle, that is, the learning rate was adjusted to 0.0005. The training results showed that the convergence speed of the model was significantly improved, and the character error rate (CER) of the prediction results for the verification set and the test set was also significantly reduced under the same epoch training.

Figure 7. Train loss on pure LaTeX formula recognition model, learning rate=0.0005 and max epoch=15.
Figure 8&9. Validation loss & CER on pure LaTeX formula recognition model, learning rate=0.0005 and max epoch=15.

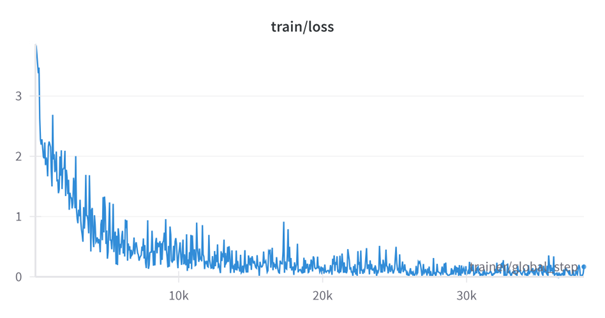
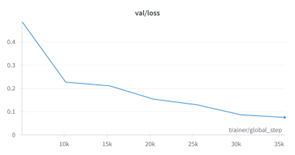
(2) The model cannot output long results due to the limitation of parameter max_output_len. Since the longest label length in the training set is 300, we increase max_output_len to 400 to meet the need to learn longer expressions.

When training the mixed recognition model of literal and mathematical expressions, we made similar parameter adjustments: the batch size was adjusted to 8, the learning rate was adjusted to 0.0003, and the remaining parameters were the same as the pure LaTeX formula recognition model.

Figure 10. Train loss on text-mixed recognition model, learning rate=0.0003 and max epoch=15.
Figure 11&12. Validation loss & CER on text-mixed recognition model, learning rate=0.0003 and max epoch=15.

Continuing Training

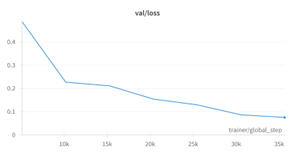
By analyzing the changes of the loss value and CER value of the model, both of them still declined relatively steadily at the end of training. Therefore, we guessed that the model had not been fully trained, and it was possible to conduct further training to improve the performance of the model. First, we tried to adjust parameters such as the learning rate, but the performance did not improve significantly, so we considered increasing the number of epochs to further optimize the model. We increase the number of epochs on the basis of the original training of the model, observe the result every two epochs, and stop the training if there are signs of overfitting. This step is quite effective for the improvement of the mixed recognition model of literal and mathematical expressions, but the performance of the pure mathematical expression recognition model is not significantly improved. We believe that this is because the mixed text and mathematical expression recognition model has a larger vocabulary and richer label information, and it needs to iteratively train all the data more times before the model can fully learn.

Hyperparameter-Tuning & Results

Model Training epoch Training dataset Testing dataset Number of decoder layers BLEU score Edit Distance score Exact Match score Overall score
Pure 15 Pure Pure 3 87.75 72.66 75.93 78.78
Pure 15 Pure Pure 5 92.26 80.06 84.58 85.64
Pure 19 Pure Pure 5 92.32 77.76 84.88 84.99
Mixed 15 Mixed Mixed 3 90.39 80.65 73.13 81.39
Mixed 21 Mixed Mixed 5 94.73 88.34 83.91 88.99
Mixed 21 Mixed Pure 5 93.90 82.46 87.21 87.86
Mixed 23 Pure (Based on 21 Mixed) Pure 5 93.16 77.11 85.99 85.42
Mixed 25 Pure (Based on 21 Mixed) Pure 5 93.20 77.05 85.95 85.40
Mixed 27 Pure (Based on 21 Mixed) Pure 5 93.20 78.23 86.08 85.84
Mixed 29 Pure (Based on 21 Mixed) Pure 5 92.95 79.97 87.44 87.12
Mixed 29 Pure (Based on 21 Mixed) Mixed 5 94.65 87.41 83.64 88.57

From the results in the table above, we find that the number of decoder layers has a great impact on the model recognition accuracy. Because of the wide variety and length of the identification formula, a deeper decoder can improve the recognition accuracy. At the same time, we observed the phenomenon of overfitting and underfitting in the model. In the pure mathematical expression recognition model, the recognition accuracy of the model with 15 epochs is higher than that with 19 epochs, and the model overfits on this data set. In the mixed recognition model of text and mathematical expressions, we tried to replace the data set for further training. For example, the model with 23 to 29 epoches showed a basinlike fluctuation in model recognition accuracy, and the recognition rate of the model with 29 epoches decreased compared with that with 21 epoches. We believe that the model has not yet learned the features of the new data set. The recognition rate decreases.

Among the above results:

  1. The optimal result of the pure mathematical expression recognition model appears at epoch 15. The loss value of the verification set is about 0.07, and the CER value of the test set reaches 0.023.

  2. The optimal result of the hybrid recognition model of literal and mathematical expressions appears at epoch 21. The loss value of the verification set is about 0.07 and the CER value of the test set reaches 0.025.

  3. We use the above two optimal models to generate prediction results on the test data identified by pure mathematical expressions and the test data identified by mixed text and mathematical expressions respectively. In addition, since the mixed text and mathematical expression recognition task logically includes the pure mathematical expression recognition task, we try to use the mixed text and mathematical expression recognition model to generate the prediction results of the test data of pure mathematical expression recognition. The scores of each evaluation index are summarized in the following table

Model Testing dataset BLEU score Edit Distance score Exact Match score Overall score
Pure Pure 92.26 80.06 84.58 85.64
Mixed Mixed 94.73 88.34 83.91 88.99
Mixed Pure 92.95 79.97 87.44 87.12

As can be seen from the table above, pure mathematical expressions that use a mixture of text and mathematical expressions to identify model predictions are better at identifying test data results than pure mathematical expressions to identify model predictions. We believe that the reason is that the training data for mixed recognition of text and mathematical expressions includes both samples of pure mathematical expressions and mixed samples of text and mathematical expressions. The training data is more diverse than that of pure mathematical expressions, and the model can learn richer information after full training. Therefore, no matter the input of mixed text and mathematical expressions, the model can learn more information. Or the input of pure mathematical expressions can give better predictions.

Conclusion

Through this identification task, we have practiced deep learning in many ways. From the selection of model architecture to data preprocessing and data loading, many attempts have been made in the process of training and parameter adjustment. In the process of trying, we also found some characteristics of deep learning, such as underfitting and overfitting. The final model test results are good.

For more information, see the work in our github repository!