This project was cooperated with Franklin-Jiang Y.J., Z.Y. Tan, Z.L. Long and W. Liu.

A. Background

We chose the Ecosphere as our topic. For humans, it is important to model the functioning of the ecosphere based on the behavior of organisms and to study the laws of it. It is of great significance to understand nature and to protect it.

In an ecosphere, there are usually multiple species with behaviors including growth, reproduction and death. The most common relation between species is predation. The predators will hunt for energy and preys may try to escape from death. The prey will also look for food to replenish its energy in a dangerous environment. If a creature has enough energy, it may reproduce next generation. However, if it lacks energy, or is predated or gets too old, it will die. In our ecospheres, it is possible for one creature to continue to flourish for a long time, or to become rapidly extinct due to the numbers of other species.

Our objective is to simulate an ecosphere. Each species in this ecosphere has behaviors like growth, reproduction and death. There species will act as predators or preys. Such a relation is reflected through predatory behavior and energy flow. We will simulate the animal behaviors mentioned above and provide GUI to visualize how the creatures behave. The user can see the chase of the predator and the escape of the prey in the window. By setting he initial number of each creature, user can observe how initial number effects the final result of ecosphere.

B. Design Principle

I. Requirement

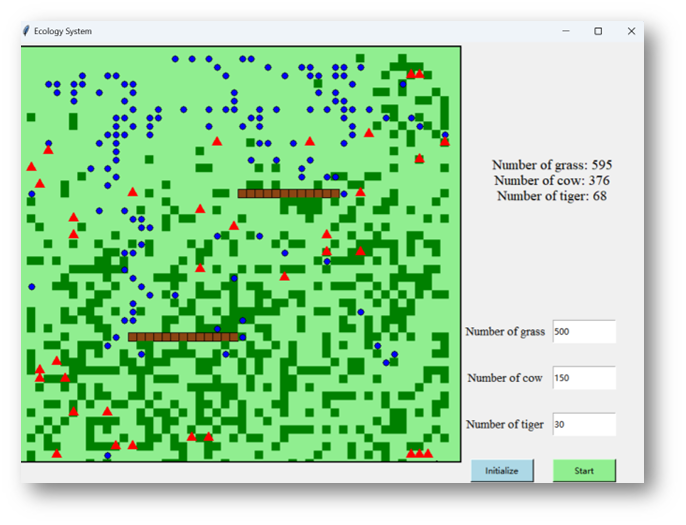
This ecosphere system is required to simulate creatures’ natural behavior. A creature will die if been preyed, or old enough. An animal will also die if it does not have enough energy. But it can search for food to get its energy, although searching and racing would cost some energy. Every species has its intrinsic characteristics and attributes, like predator, another species as food source, cost of been preyed, energy gain after being preyed, life-span and initial number. As minimum requirements, grass, cow and tiger should be included in the ecosphere program. In addition, a GUI is needed to provide interactive visualization window for user, where each creature is presented as dots with different color and shape.

II. Function

In our system, user can set the initial number of each species and run the program to observe how the animal act and how the number of each species change as time passing by in ecosphere system. With GUI, user can watch animals chasing for food or running away from predator, they calculate the optimal path with A* algorithm and hen run follow this path.

III. Assumptions

1. When a new ecosphere is initialized, creatures randomly and evenly appear on the map. The age of organisms obeys a normal distribution from 0 to half of the life span and the energy obeys a normal distribution from half of the maximum energy to maximum energy.
2. Each creature has a maximum number. They will not reproduce when total amount of that creature reaches the upper bound.
3. It does not take time to eat the food.
4. Predators only chase the nearest prey.
5. The predator can eat the predator directly within a certain distance.
6. The predator can get all the energy of the prey if it catches the prey.
7. Creatures do not choose to find food when their energy is full.
8. The life span and reproduce rate of each species is fixed.
9. Animals and plants reproduce asexually.
10. The energy of an individual is reduced by half due to reproduction of offspring.
11. The requirements for reproduction are that the energy of the individual is greater than one third of the maximum energy, and that the age is greater than one fifth of the life span.

C. Path-Finding Algorithms

We deployed A* Algorithm for path-finding.

A* (A-STAR) algorithm is the most effective direct search method to solve the shortest path in the static road network, and it is also an effective algorithm to solve many search problems. The closer the distance estimate in the algorithm is to the actual value, the faster the final search speed. The algorithm’s estimation function can be presented as the formula below:

where f(x) represents the minimum cost estimate from the initial state through state x to the target state. g(x) represents the minimum cost of going from the initial state to state x in the state space. h(x) represents the minimum estimated cost of the path from state x to the destination state.

A* is considered as a heuristic searching method. The information for searching is within the heuristic function h(x). It is considered to be an expansion method from the Dijkstra algorithm.

There are many kinds of heuristic functions. We aimed to choose a suitable one that not only satisfies the searching job but also simple enough for the computer to execute. Since there will be bunch of calculations in one period of loop, the heuristic function cannot be much complicated.

Eventually, we designed the heuristic function using a specific method called Octile Distance. It is a very suitable optimization model for Diagonal distance because Octile distance only allows 45 degrees’ turning and straight lines. The heuristic function using Octile distance is shown as below:

* Initialize open_set and close_set;
* Add the starting point to open_set and set the priority to 0 (highest priority);
* If open_set is not empty, the node n with the highest priority is selected from open_set:
  * If node n is the end point, then:
    * Trace the parent node step by step from the end to the beginning;
    * Return the found result path, the algorithm ends;
  * If node n is not the end point, then:
    * Remove node n from open_set and add it to close_set;
    * Iterate over all neighboring nodes of node n:
    * If the adjacent node m is in close_set, then:
      * Skip and select the next adjacent node
    * If the adjacent node m is also not in open_set, then:
      * Set the parent of node m to node n
      * Compute the priority of node m
      * Add node m to open_set

As the pseudo code provided above, the A* Algorithm is implemented. Where open set contains the points that are going to be expanded, while close set contains the points that have been visited. By iterating the tree reversely after the end point is reached, a path can be found. Obviously, in some extreme situations, the heuristic function h(x) maintains 0, then the algorithm is a pure Dijkstra Algorithm. The A* algorithm selects the node with the lowest f(n) value (highest priority) from the priority queue each time as the next node to be traversed.

Depth-Limited Modified A* Algorithm

However, A* algorithm shows some weakness in practice. There may exist cycles in the search graph generated by A*, which means it will go into an infinite loop and never come out. Thus, we modified the A* algorithm again by limiting the depth in looping. As a result, the A* algorithm practices well. Additionally, those situations where A* cannot find a solution within the depth limitation are considered to be not possible path found.

For more information, see the work in our github repository!